Définition de la fonction exponentielle de base e (1)

Théorème

Il existe une unique fonction exponentielle telle que : 

• l'image de `0` est égale à `1` ;
• le coefficient directeur de la tangente à la courbe au point d'abscisse \(0\) est égal à \(1\).
  

Remarque

Dire que l'image de `0` par une fonction est égale à `1` équivaut à dire que la courbe représentative de cette fonction passe par le point \(\text{A}(0~;1)\).

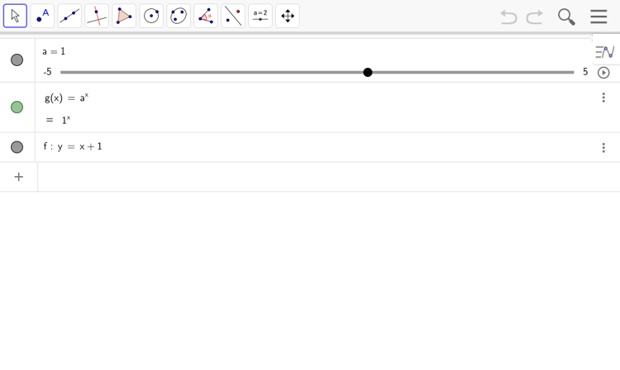
Illustration

Le fichier de géométrie dynamique suivant permet de conjecturer la valeur du réel `a`, base de la fonction exponentielle objet du théorème précédent. Il permet de trouver une valeur approchée de \(a\).